LeetCode 221. Maximal Square

221. Maximal Square

Given an m x n binary matrix filled with 0's and 1's, find the largest square containing only 1's and return its area.

 

Example 1:

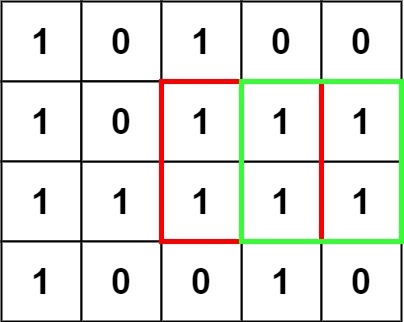
Input: matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
Output: 4

Example 2:

Input: matrix = [["0","1"],["1","0"]]
Output: 1

Example 3:

Input: matrix = [["0"]]
Output: 0

 

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 300
• matrix[i][j] is '0' or '1'.

	class Solution {
	public:
	/**
	Framework
	1. State & Function
	state vars: (i, j) i = ver, j = hor
	dp[row][col]: largest square, matrix[row][col] is square's right bottom corner
	2. Relation
	dp[i][j] = dp[i-1][j] == dp
	3. Base
	*/
	int maximalSquare(vector<vector<char>>& matrix) {
	int m = matrix.size();
	int n = matrix[0].size();
	vector<vector<int>> dp(m + 1, vector<int>(n + 1));
	int ans = 0;
	for(int i = 1; i <= m; i++){
	for(int j = 1; j <= n; j++){
	if(matrix[i-1][j-1] == '0')
	continue;
	// relation
	dp[i][j] = min({dp[i][j-1], dp[i-1][j], dp[i-1][j-1]}) + 1;
	// update ans
	ans = max(ans, dp[i][j] * dp[i][j]);
	}
	}
	return ans;
	}
	};

view raw 221. Maximal Square.cpp hosted with ❤ by GitHub