LeetCode 311. Sparse Matrix Multiplication

 311. Sparse Matrix Multiplication

Given two sparse matrices mat1 of size m x k and mat2 of size k x n, return the result of mat1 x mat2. You may assume that multiplication is always possible.

 

Example 1:

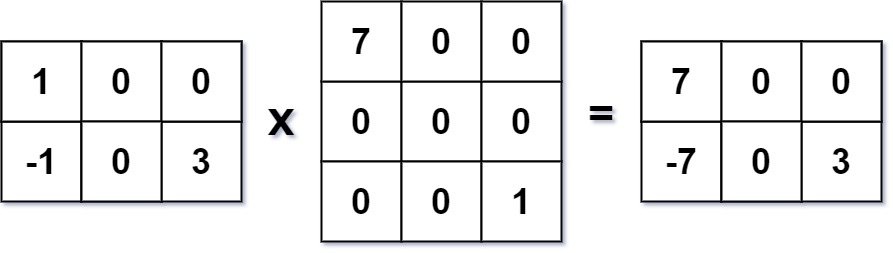
Input: mat1 = [[1,0,0],[-1,0,3]], mat2 = [[7,0,0],[0,0,0],[0,0,1]]
Output: [[7,0,0],[-7,0,3]]

Example 2:

Input: mat1 = [[0]], mat2 = [[0]]
Output: [[0]]

 

Constraints:

• m == mat1.length
• k == mat1[i].length == mat2.length
• n == mat2[i].length
• 1 <= m, n, k <= 100
• -100 <= mat1[i][j], mat2[i][j] <= 100