LeetCode 542. 01 Matrix

 542. 01 Matrix

Given an m x n binary matrix mat, return the distance of the nearest 0 for each cell.

The distance between two adjacent cells is 1.

 

Example 1:

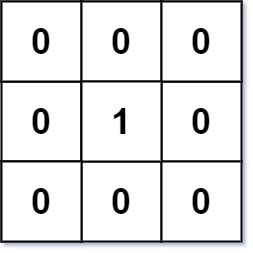
Input: mat = [[0,0,0],[0,1,0],[0,0,0]]
Output: [[0,0,0],[0,1,0],[0,0,0]]

Example 2:

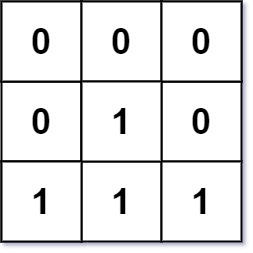
Input: mat = [[0,0,0],[0,1,0],[1,1,1]]
Output: [[0,0,0],[0,1,0],[1,2,1]]

 

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 104
• 1 <= m * n <= 104
• mat[i][j] is either 0 or 1.
• There is at least one 0 in mat.

	class Solution {
	public:
	vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
	queue<pair<int, int>> q;
	int n = mat.size();
	int m = mat[0].size();
	vector<vector<int>> f(n, vector<int>(m, INT_MAX - 1e4));
	// first pass: top-down
	for(int i = 0; i < n; i++)
	for(int j = 0; j < m; j++){
	if(mat[i][j] == 0){
	f[i][j] = 0;
	} else {
	if(i > 0)
	f[i][j] = min(f[i][j], f[i-1][j] + 1);
	if(j > 0)
	f[i][j] = min(f[i][j], f[i][j-1] + 1);
	}
	}
	// second pass: bottom-up
	for(int i = n - 1; i >= 0; i--)
	for(int j = m - 1; j >= 0; j--){
	if(mat[i][j] == 0){
	f[i][j] = 0;
	} else {
	if(i < n - 1)
	f[i][j] = min(f[i][j], f[i+1][j] + 1);
	if(j < m - 1)
	f[i][j] = min(f[i][j], f[i][j+1] + 1);
	}
	}
	return f;
	}
	};

view raw 542. 01 Matrix.cpp hosted with ❤ by GitHub